Astronomy & Astrophysics manuscript no. PTsym_in_astro ©ESO 2024
May 30, 2024
PT and anti-PT symmetries for astrophysical waves
Armand Leclerc1,⋆, Guillaume Laibe1, and Nicolas Perez1
Univ Lyon, Univ Lyon1, Ens de Lyon
CNRS, Centre de Recherche Astrophysique de Lyon UMR5574
F-69230, Saint-Genis,-Laval, France
Received September 15, 1996; accepted March 16, 1997
ABSTRACT
Context. Discrete symmetries have found numerous applications in photonics and quantum mechanics, but remain little studied in fluid mechanics, particularly in astrophysics.
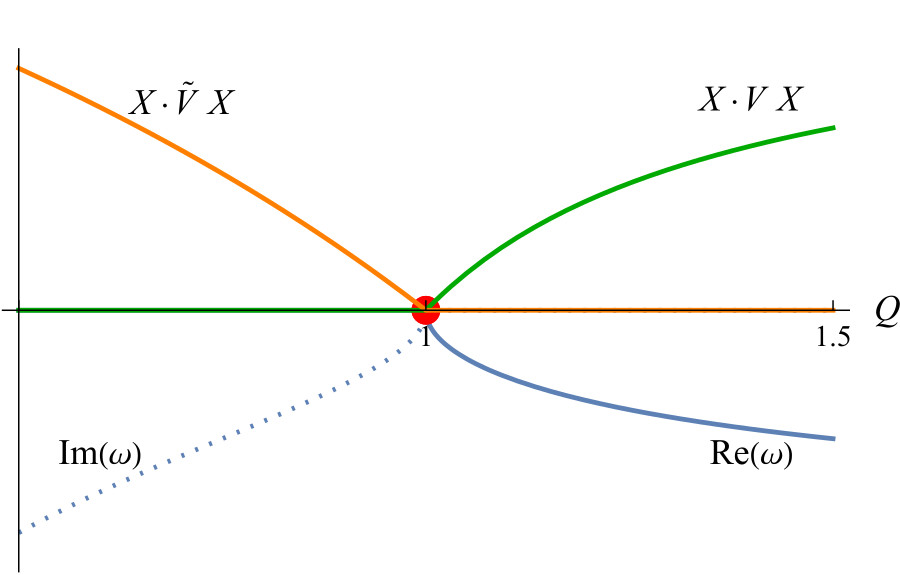
Aims. We aim to show how PT and anti-PT symmetries determine the behaviour of linear perturbations in a wide class of astrophys- ical problems. They set the location of Exceptional Points in the parameter space and the associated transitions to instability, and are associated to the conservation of quadratic quantities that can be determined explicitly. Methods. We study several classical local problems: the gravitational instability of isothermal spheres and thin discs, the Schwarzschild instability, the Rayleigh-Bénard instability and acoustic waves in dust-gas mixtures. We calculate the locations and the order of the Exceptional Points with a method of resultant, as well as the conserved quantities in the different regions of the parameter space using Krein theory. Results. All problems studied here exhibit discrete symmetries, even though Hermiticity is broken by different physical processes
(self-gravity, buoyancy, diffusion, drag). This analysis provides genuine explanations for certain instabilities, and for the existence of regions in the parameter space where waves do not propagate. Those correspond to breaking of PT and anti-PT symmetries respectively. Not all instabilities are associated to symmetry breaking (e.g. the Rayleigh-Benard instability).