T. Santos, T. Bodin, F. Soulez, Y. Ricard and Y. Capdeville
Geophysical Journal International, Volume 238, Issue 3, September 2024, Pages 1676–1695
https://doi.org/10.1093/gji/ggae240
SUMMARY
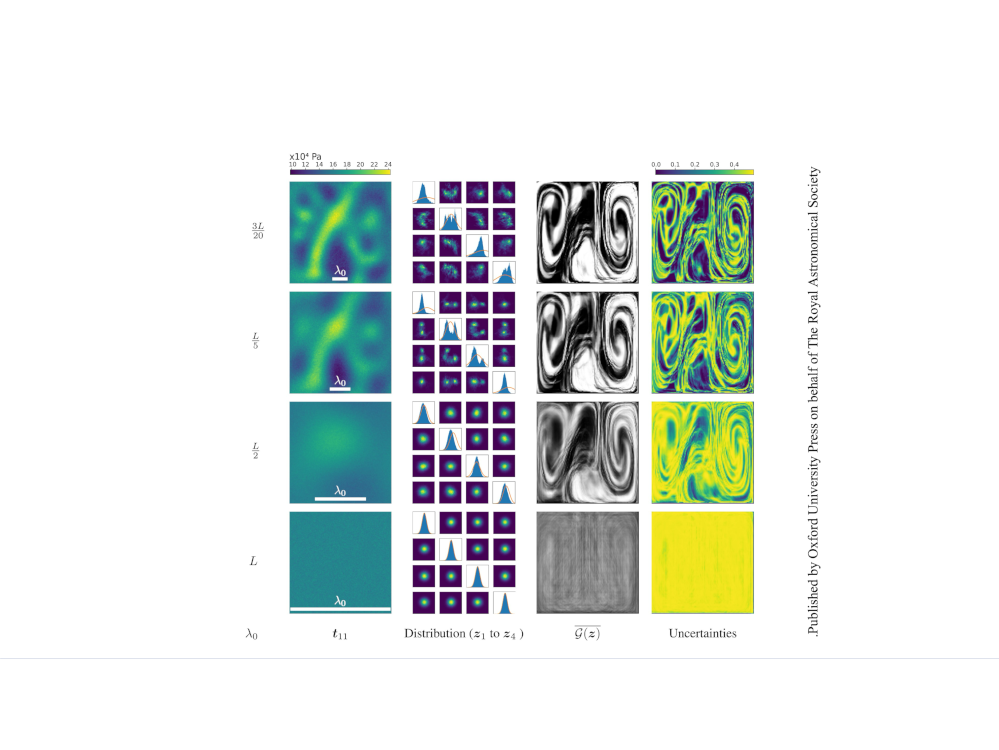
Inverse problems occur in many fields of geophysics, wherein surface observations are used to infer the internal structure of the Earth. Given the non-linearity and non-uniqueness inherent in these problems, a standard strategy is to incorporate a priori information regarding the unknown model. Sometimes a solution is obtained by imposing that the inverted model remains close to a reference model and with smooth lateral variations (e.g. a correlation length or a minimal wavelength are imposed). This approach forbids the presence of strong gradients or discontinuities in the recovered model. Admittedly, discontinuities, such as interfaces between layers, or shapes of geological provinces or of geological objects such as slabs can be a priori imposed or even suggested by the data themselves. This is however limited to a small set of possible constraints. For example, it would be very challenging and computationally expensive to perform a tomographic inversion where the subducting slabs would have possible top discontinuities with unknown shapes. The problem seems formidable because one cannot even imagine how to sample the prior space: is each specific slab continuous or broken into different portions having their own interfaces? No continuous set of parameters seems to describe all the possible interfaces that we could consider. To circumvent these questions, we propose to train a Generative Adversarial neural Network (GAN) to generate models from a geologically plausible prior distribution obtained from geodynamic simulations. In a Bayesian framework, a Markov chain Monte Carlo algorithm is used to sample the low-dimensional model space depicting the ensemble of potential geological models. This enables the integration of intricate a priori information, parametrized within a low-dimensional model space conducive to efficient sampling. The application of this approach is demonstrated in the context of a downscaling problem, where the objective is to infer small-scale geological structures from a smooth seismic tomographic image.